The Watermelon Problem

Prologue

Curriculum and Connections [file unavailable] Expectations: Fractions

• use fraction skills in solving problems involving measurement

Part 1: Entry

To introduce the problem, I just brought in a watermelon and sat it on the table until students had enough questions. Once they were ready, I put "What do you want to know?" on the board, and as they asked questions, I gave them markers so they could put their questions on the board.

Based on these questions, students decided to study the problem, "How can you cut up the watermelon so that each of the 27 students can have an equal slice?"

Part 2: Attack

Here are some resources for the watermelon we chose. It's honestly better to get your own watermelon though.

Here are some examples of student work and ideas. Many of them came up with some form of idea to do a third of a third of a third.

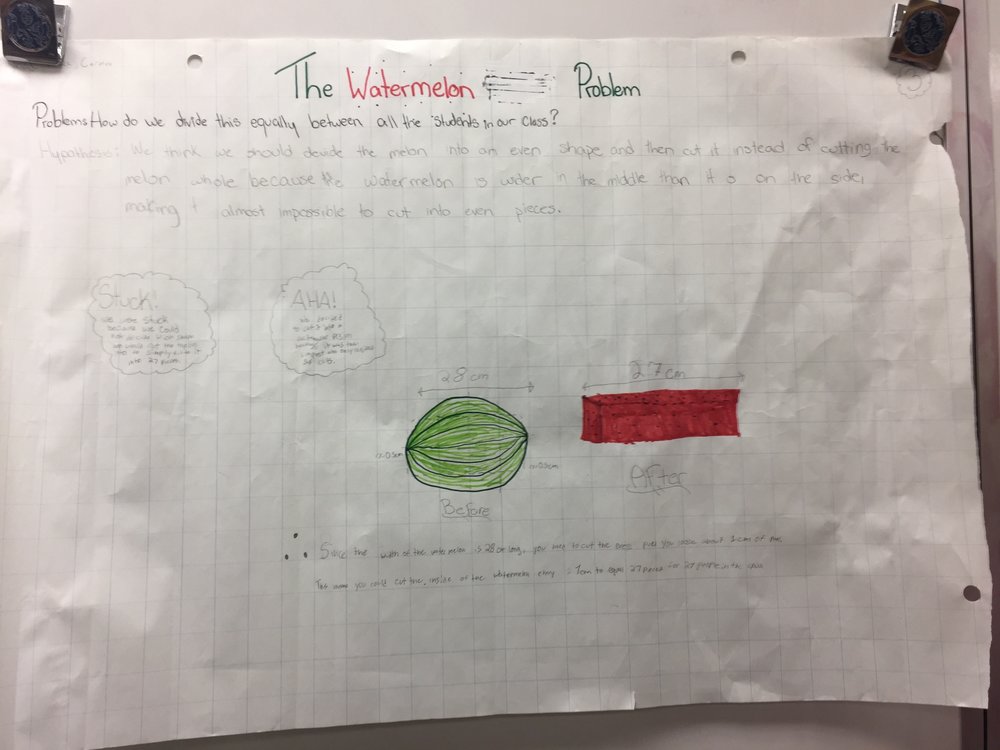
Part 3(a,b): Review (Check, Reflect)

After finishing this problem, it's time for students to check if the solution worked the way they expected, and to reflect on what went well and what can be improved on. You can see in the video that cutting the watermelon into thirds would require a very high level of precision to do well. There are a whole bunch of hindrances. For the sequel, encourage students to find a better way to divide the watermelon. Can they add the precision necessary to cut the slices precisely equally? Can they find a better way to distribute the watermelon?

Part 3(c): Review (Extend)

Once students are ready, they can try to find a strategy that can work easily for any number of students.

Elements of Solutions

Here is one possible such strategy. The result is pretty easy to generalize to any number of students. However, there are still a couple of precision-related problems with this strategy.

Here is a different strategy. Still pretty easy to generalize to any number of students, but with different pros and cons.